About DendroTweaks

DendroTweaks is a toolbox designed to facilitate the creation and validation of single-cell biophysical models. With its user-friendly interface and diverse set of tools, researchers can deepen their understanding of how the morphological and biophysical properties of a neuron impact its somatic and dendritic voltage dynamics.

For a quick overview of the toolbox, including a video demonstration, you can visit our e-poster presented at the FENS Forum 2024 in Vienna.

Key Features

Interactive adjustments

DendroTweaks allows you to adjust any parameter of the model and receive real-time visual feedback. With widgets and interactive plots, you can explore the impact of different morphological and biophysical parameters on the voltage dynamics of a neuron.

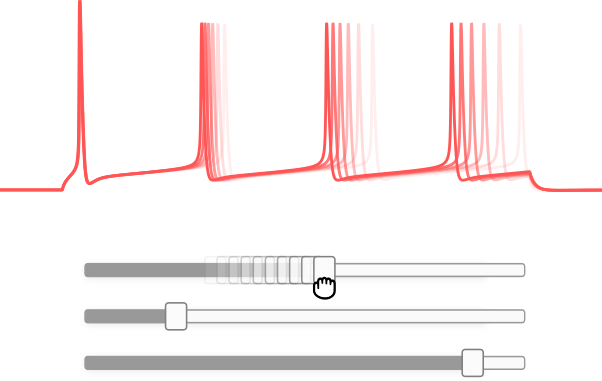
Standardization of ion channel models

You can automaticlly parse existing .mod files and adjust channel kinetics with interactive widgets. Additionaly, we provide the means to standardize ion channel models by fitting a set of equations [1] to the original activation curves.

Standard equations for kinetics of voltage-gated ion channels

Current for a given ion channel: $$I = \bar{g} \times p(x_1, ..., x_n) \times (V_m - E) \tag{1}$$

where:

• $\bar{g}$ — the maximum conductance in $S/cm^2$
• $p(x_1, ..., x_n)$ — the open probability of the channel
• $V_m$ — the membrane potential in $mV$
• $E$ — the equilibrium potential in $mV$

Time derivative of a state variable: $$\dot{x} = \dfrac{x^{\infty} - x}{\tau_x} \tag{2}$$

Steady state: $$x^{\infty} = \dfrac{1}{1 + \exp \left({-\dfrac{V - V_{half}}{\sigma}}\right)} \tag{3}$$

Time constant: $$\tau_x = \dfrac{1}{\alpha'(V) + \beta'(V)} + \tau_0 \tag{4}$$

where $$\alpha'(V) = K \times \exp \left({\dfrac{\delta \times (V - V_{half})}{\sigma}}\right) \tag{5}$$ $$\beta'(V) = K \times \exp \left({\dfrac{-(1 -\delta) \times (V_{half} - V)}{\sigma}}\right) \tag{6}$$

where:

• $V$ — the membrane potential in $mV$
• $V_{half}$ — the half-activation potential in $mV$
• $\sigma$ — the inverse slope in $mV$
• $\delta$ — the skew parameter of the time constant curve (unitless)
• $K$ — the maximum rate parameter in $ms^{-1}$
• $\tau_0$ — the rate-limiting factor (minimum time constant) in $ms$

Morphology reduction

You can reduce neuronal morphology by simplifying the dendritic structure. We have extended the functionality of neuron_reduce [2] to allow for an arbitrary level of morphology reduction.

Automatic validation

Our toolbox provides a set of built-in validation protocols to ensure the model's activity is consistent with the experimental data.

References

• Principles of Computational Modelling in Neuroscience (Sterratt, D. et al.; 2011)
• Amsalem, O., Eyal, G., Rogozinski, N. et al. An efficient analytical reduction of detailed nonlinear neuron models. Nat Commun 11, 288 (2020).
  https://doi.org/10.1038/s41467-019-13932-6